第零章：学习算法和刷题的框架思维
labuladong
LeetCode
发布日期:   2020-07-23
作者:   M
文章字数:   3.1k
阅读时长:   15 分
热度:  

labuladong学习算法和刷题的框架思维

124. 二叉树中的最大路径和_后序遍历

  • 采用后序遍历：先访问左子树，再访问右子树，最后根据左右子树的结果和当前节点更新当前节点对应的最大值
  • maxVal 记录的是全局最大路径和（可以不返回，因为它始终在递归过程中更新即可，递归结束时，这个值也就出来了）
  • 定义递归函数的意义：
    • 定义dfs函数：返回root的左（或右）子树能向root节点“提供”的最大路径和。即，一条从父节点延伸下来的路径，能在当前子树中获得的最大收益。也就是：dfs()函数返回的是包含root在内的单边最大路径和。分为三种情况：
      • 路径停在当前子树的根节点，在这个子树中收益：root.val
      • 走入左子树，在这个子树中的最大收益：root.val + dfs(root.left)
      • 走入右子树，在这个子树中的最大收益：root.val + dfs(root.right)
  • 若root的左节点对应的最大路径和是负数（在拖后腿，所以抛弃），则最大路径和为0，因此有l=max(0,dfs(root.left))。右节点同理
  • 记得写递归结束的条件

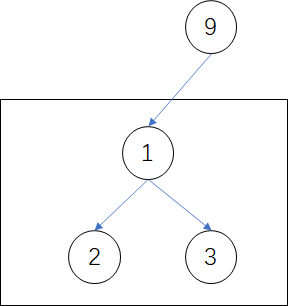
Q：为什么递归函数返回的是以根节点为首的单边最大路径和，而不是两边最大路径和？
A：若以1为根节点，它对应的最大路径和当然是1+2+3。但对于9而言，1作为9的左子树，1节点只能提供1+3（单边最大路径和），而不能提供1+2+3，否则1+2+3+9会产生路径重复。因此递归函数要返回单边最大路径和，而递归过程中不断更新全局最大路径和self.maxVal=max(self.maxVal,root.val+l+r)
20210617095226

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def maxPathSum(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        def dfs(root):
            if not root:return 0
            # 后序遍历：左
            l=max(0,dfs(root.left))
            # 后序遍历：右
            r=max(0,dfs(root.right))
            # 后序遍历：中，实现最大值的更新
            self.maxVal=max(self.maxVal,root.val+l+r)
            # 递归函数返回： 从根节点延生下来的一条路径
            return root.val+max(l,r)

        self.maxVal=float("-inf")
        dfs(root)
        return self.maxVal
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):

    def __init__(self):
        self.ans = float("-inf")
    def help(self,root):
        if not root: return 0
        l=max(0,self.help(root.left))
        r=max(0,self.help(root.right))
        self.ans=max(self.ans, root.val + l + r)
        return root.val+max(l,r)
    def maxPathSum(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        # self.ans=float("-inf")
        self.help(root)
        return self.ans

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
//    定义全局变量
    int maxVal = INT_MIN;
//dfs函数返回某个子树+当前节点对应的   单边最大和
    int dfs(TreeNode *root) {
        if (root == nullptr)
            return 0;
        int l = max(0, dfs(root->left));
        int r = max(0, dfs(root->right));
        maxVal = max(maxVal, root->val + l + r);
        return root->val + max(l, r);
    }

    int maxPathSum(TreeNode *root) {
        dfs(root);
        return maxVal;
    }
};

类似题目104. 二叉树的最大深度_后序遍历

  • dfs()函数返回包含root在内的二叉树最大深度
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        def dfs(root):
            if not root: return 0
            l=dfs(root.left)
            r=dfs(root.right)
            return max(l,r)+1
        return dfs(root)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int dfs(TreeNode *root) {
        if (root == nullptr)
            return 0;
        int l = dfs(root->left);
        int r = dfs(root->right);
        ans = max(l, r) + 1;
        return ans;

    }

    int ans = 0;

    int maxDepth(TreeNode *root) {
        return dfs(root);
    }
};

//或者直接写：
class Solution {
public:
    int maxDepth(TreeNode *root) {
        if (root == nullptr)
            return 0;
        int l = maxDepth(root->left);
        int r = maxDepth(root->right);
        return max(l, r) + 1;
    }
};

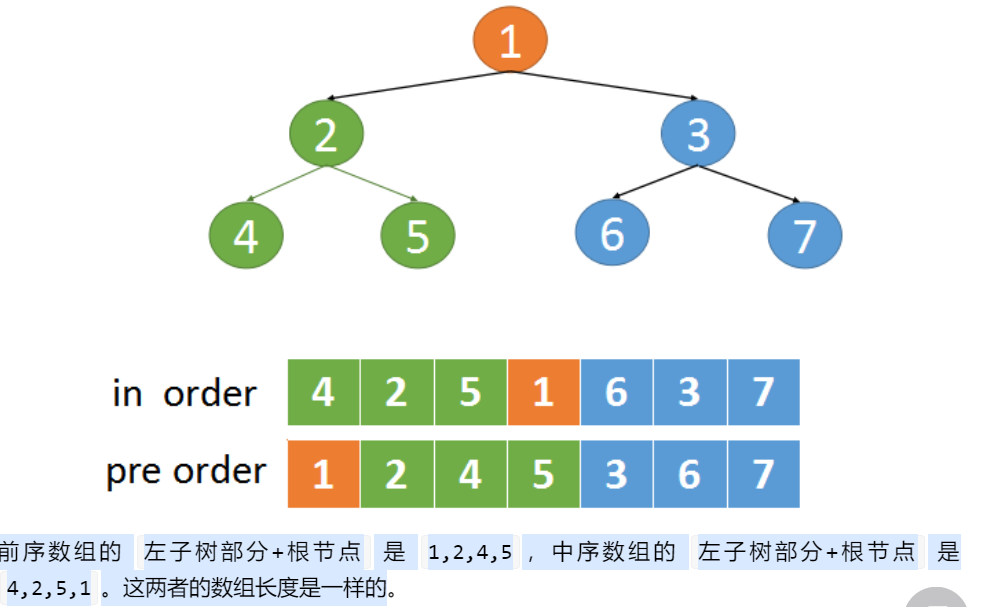
105. 从前序与中序遍历序列构造二叉树_前序遍历


图片来源

树的前序遍历：先构造根节点，基于根节点的信息找到左右子树的preorder和inorder范围，然后分别处理左右子树

  • 前序遍历的第一个元素是根节点
  • 在中序遍历中找到根节点的位置，其左边的元素就是左子树，右边的元素就是右子树
  • 然后递归处理左右子树
  • 注意写上递归结束条件（左右子树为空时）
  • 前序数组怎么切分呢？前序数组的 （左子树部分+根节点） 长度 和 中序数组的 （左子树部分+根节点） 长度是一样的
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        if not (preorder and inorder):return None
        root=TreeNode(preorder[0])# 前序遍历：根   构造根节点
        midIdx=inorder.index(root.val)
        # 递归处理左右子树
        root.left=self.buildTree(preorder[1:midIdx+1],inorder[:midIdx])# 前序遍历：左
        root.right=self.buildTree(preorder[midIdx+1:],inorder[midIdx+1:])# 前序遍历：右
        return root

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (preorder.size() == 0 ||inorder.size()==0)
            return NULL;

        TreeNode *root=new TreeNode(preorder[0]);
        int midIdx=0;
        while (inorder[midIdx]!=root->val)
            midIdx++;
        vector<int> preorder_l(preorder.begin()+1,preorder.begin()+midIdx+1);
        vector<int> preorder_r(preorder.begin()+midIdx+1,preorder.end());

        vector<int> inorder_l(inorder.begin(),inorder.begin()+midIdx+1);
        vector<int> inorder_r(inorder.begin()+midIdx+1,inorder.end());

        root->left= buildTree(preorder_l,inorder_l);
        root->right= buildTree(preorder_r,inorder_r);
        return root;
    }
};

99. 恢复二叉搜索树_中序遍历

题目说二叉搜索树，中序遍历后应该是升序排列。否则若出现非递增的元素，说明这个地方有错误

  • 先中序遍历二叉搜索树，保存在nodes列表中（列表中的元素是节点）
  • pre保存遍历过程中i的前一个节点。如果发现异常，标定出
  • 找到错误节点x、y后，交换x与y的值

方法1：递归

  • 不要跳进递归，定义递归函数的意义并相信它能实现自己的功能 （注意加上递归结束的条件）
    • 递归函数的功能：记录异常点出现的位置,并且更新pre，使得pre始终在root前面
    • 中序遍历左；
    • 中序遍历中：找到两个变化的点，第一个点赋值pre，第二个点赋值root。及时记录并更新pre（这样，在后面的中序遍历右时，pre的值为根节点的值，可以进行新一轮的递归和比较）
    • 中序遍历右
    • 交换两个点的数值

注意!!!!!!

            
            if self.pre!=None:
                 
        
        self.pre=None

  • 在dfs函数中，一定要判断if self.pre!=None:，

  • （原因）为了能够递归起来，需要确保self.pre!=None（因为初始化 self.pre=None）

  • 否则在执行if self.fir == None and self.pre.val >= root.val:时，编译器都不确定self.pre成不成立，更别说self.pre.val了；

  • 在c++中同理

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def recoverTree(self, root):
        """
        :type root: TreeNode
        :rtype: None Do not return anything, modify root in-place instead.
        """
        # 中序遍历
        def dfs(root):
            if not root: return
            # 中序遍历：左
            dfs(root.left)

            # 中序遍历：中
            # 找到两个左大右小的地方，第一个地方把pre赋给fir，第二个地方把root赋给sec
            if self.pre!=None: # 在递归过程中，pre不断进行更新，始终指向当前节点的前一个（不是物理空间的前面，是中序遍历顺序的前面）节点
                if self.fir == None and self.pre.val >= root.val:
                    self.fir = self.pre
                if self.fir != None and self.pre.val >= root.val:
                    self.sec = root
            # pre为root前面（不是物理空间的前面，是中序遍历顺序的前面）的节点
            # 在下次进入dfs(root)入口前，及时记录并更新pre
            self.pre = root

            # 中序遍历：右
            dfs(root.right)


        self.fir = None
        self.sec = None
        self.pre=None
        dfs(root)
        # 交换两个地方的值
        self.fir.val,self.sec.val=self.sec.val,self.fir.val

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

class Solution {
public:
    TreeNode *fir = nullptr;
    TreeNode *sec = nullptr;
    TreeNode *pre = nullptr;

    void dfs(TreeNode *root) {
//        递归结束的条件
        if (!root)
            return;
//        中序遍历：左
        dfs(root->left);
//        中序遍历：中
        if (pre != nullptr) {
            if (fir == nullptr && pre->val >= root->val) fir = pre;
            if (fir != nullptr && pre->val >= root->val) sec = root;
        }
        pre = root;
//        中序遍历：右
        dfs(root->right);
    }

    void recoverTree(TreeNode *root) {
        dfs(root);
        int tmp = fir->val;
        fir->val = sec->val;
        sec->val = tmp;

    }
};

P.S., 以下供参考：

  • 在测试用例不严格的情况下，可以对pre赋一个最小的值，然后在dfs中对其更新，这样就不用判断pre是否合法了
    • 在python中可以通过
    • 在c++中，由于有个测试用例中包括了INT_MIN,所以会报错，可以把pre 置为空指针
# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def recoverTree(self, root):
        """
        :type root: TreeNode
        :rtype: None Do not return anything, modify root in-place instead.
        """
        self.fir=None
        self.sec=None
        self.pre=TreeNode(float("-inf"))


        def dfs(root):
            if not root:
                return
            dfs(root.left)

            if self.fir==None and self.pre.val>root.val:
                self.fir=self.pre
            if self.fir and self.pre.val>=root.val:
                self.sec=root
            self.pre=root

            dfs(root.right)
        dfs(root)
        self.fir.val,self.sec.val=self.sec.val,self.fir.val

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

class Solution {
public:
    TreeNode *fir = nullptr;
    TreeNode *sec = nullptr;
    TreeNode *pre = new TreeNode(INT_MIN);

    void dfs(TreeNode *root) {
//        递归结束的条件
        if (!root)
            return;
//        中序遍历：左
        dfs(root->left);
//        中序遍历：中

            if (fir == nullptr && pre->val >= root->val) fir = pre;
            if (fir != nullptr && pre->val >= root->val) sec = root;
           // 也可以这样
            //if (pre->val >= root->val) {
            //  fir = (fir == nullptr) ? pre : fir;
            //   sec = root;
          // }

        pre = root;
//        中序遍历：右
        dfs(root->right);
    }

    void recoverTree(TreeNode *root) {
        dfs(root);
        int tmp = fir->val;
        fir->val = sec->val;
        sec->val = tmp;

    }
};

方法2：遍历一次树，保存到数组中，再进行判断

微信图片_20210617185623

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def recoverTree(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        nodes=[]# nodes 中保存节点
        # 中序遍历二叉树,得到递增序列
        def dfs(root):
            if not root: return
            dfs(root.left)
            nodes.append(root)
            dfs(root.right)
        dfs(root)

        # 如果出现非递增的元素，说明这个地方有错误
        x=None
        y=None
        pre=nodes[0]
        for i in range(1,len(nodes)):
            if pre.val>nodes[i].val:
                y=nodes[i]
                if not x:
                    x=pre
            pre=nodes[i]

        # 交换x与y的值
        if x and y:
            x.val,y.val=y.val,x.val

或者

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def recoverTree(self, root):
        """
        :type root: TreeNode
        :rtype: None Do not return anything, modify root in-place instead.
        """
        node = []
        # 中序遍历把节点保存在列表中
        def dfs(root):
            if not root: return
            dfs(root.left)
            node.append(root)
            dfs(root.right)

        dfs(root)
        pre = node[0]
        n = len(node)
        x = None
        y = None
        for i in range(1, n):
            # 第一次左大右小，保存左
            if (not x) and pre.val > node[i].val:
                x = pre
            # 第二次左大右小，保存右
            if x and pre.val > node[i].val:
                y = node[i]
            pre = node[i]
        # 交换值
        if x and y:
            x.val, y.val = y.val, x.val

注意！！！！！！

  • TreeNode *fir = nullptr; 和TreeNode *sec = nullptr; 一定要赋初值nullptr，否则指针会乱指
  • 传到dfs中的是nodes的引用 （当然也可以把nodes置为全局变量）
class Solution {
public:

//    注意这里传的是nodes的引用
    void dfs(TreeNode *root, vector<TreeNode *> &nodes) {
        if (root == NULL)
            return;
        dfs(root->left, nodes);
        nodes.push_back(root);
        dfs(root->right, nodes);
    }

    void recoverTree(TreeNode *root) {
        vector < TreeNode * > nodes;
        dfs(root, nodes);
//这里要给指针赋初值，否则它会乱指到其他地方
        TreeNode *fir = nullptr;
        TreeNode *sec = nullptr;

        for (int i = 0; i < nodes.size() - 1; ++i) {
            if (nodes[i]->val > nodes[i + 1]->val) {
                sec = nodes[i + 1];
                if (fir == NULL) {
                    fir = nodes[i];
                }
            }
        }
        if (fir != nullptr && sec != nullptr) {
            int tmp = fir->val;
            fir->val = sec->val;
            sec->val = tmp;
        }
    }
};

其他写法：

class Solution {
public:
    vector<TreeNode *> nodes;

    void dfs(TreeNode *root) {
        if (root == NULL)
            return;
        dfs(root->left);
        nodes.push_back(root);
        dfs(root->right);
    }

    void recoverTree(TreeNode *root) {
        dfs(root);
        TreeNode *fir= nullptr;
        TreeNode *sec= nullptr;
//        TreeNode *pre = new TreeNode(INT_MIN);
        TreeNode *pre= nullptr;
        for (int i = 0; i < nodes.size(); i++) {
            if (pre){
            if (pre->val >= nodes[i]->val) {
                sec = nodes[i];
                if (!fir)
                    fir = pre;
            }}
            pre = nodes[i];
        }


        if (fir != nullptr && sec != nullptr) {
        int tmp = fir->val;
        fir->val = sec->val;
        sec->val = tmp;}
    }
};
赏

   转载规则


《第零章：学习算法和刷题的框架思维》 由 M 采用 知识共享署名 4.0 国际许可协议 进行许可。
 上一篇
第零章：动态规划解题套路框架 第零章：动态规划解题套路框架
labuladong动态规划解题套路框架 动态规划之背包汇总 第零章：动态规划解题套路框架第一章：经典动态规划：0-1 背包问题第零章：经典动态规划：子集背包问题第零章：经典动态规划：完全背包问题 动态规划一般采用自底向上的方式求最值。
2020-07-24 LeetCode
labuladong
下一篇 
Python经典排序算法 Python经典排序算法
Python经典排序算法 Complete Beginner’s Guide to Big O Notation 选择排序 对每一个nums[i], 寻找 $range(i,n)$ 范围内比nums[i]大的数，并与之交换 以此类推，位置
2020-07-22 LeetCode
LeetCode
  目录