labuladong

LeetCode

发布日期: 2020-07-24

作者: M

文章字数: 3.7k

阅读时长: 17 分

热度:

labuladong回溯算法解题套路框架

解决一个回溯问题，实际上就是一个决策树的遍历过程。主要考虑的问题有：

路径：也就是已经做出的选择。

选择列表：也就是你当前可以做的选择。

结束条件：也就是到达决策树底层，无法再做选择的条件。

回溯算法的框架：
（在想这个框架时，心里先建立一个N叉递归决策树，在每个决策点做选择）

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        # 做选择, 类似前序遍历
        将该选择从选择列表移除
        路径.add(选择)
        backtrack(路径, 选择列表)
        # 撤销选择，类似后序遍历
        路径.remove(选择)
        将该选择再加入选择列表

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」。
for循环的一开始，往往先用if ...continue语句跳过不合法的选择（来更新选择列表）
可以把「路径」和「选择」列表作为决策树上每个节点的属性。

以全排列为例，这张图）非常清晰地说明了路径和选择列表的关系（加入路径后，选择也相应减少）。
backtrack 函数其实就像一个指针，在这棵树上游走，同时要正确维护每个节点的属性，每当走到树的底层，其「路径」就是一个全排列。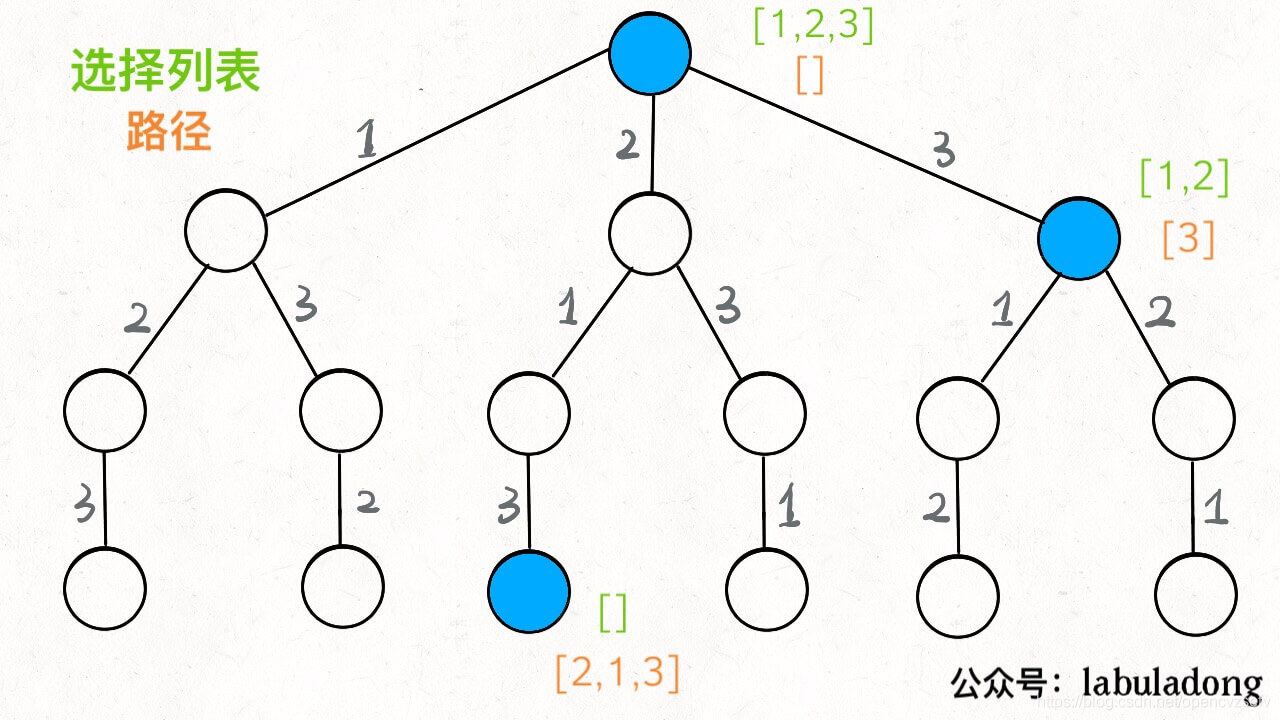

46. 全排列

res保存整体结果，visited保存已经走过的路径
for 循环的一开始，利用 if num in visited: continue 可巧妙地更新选择列表（通过continue跳出此次循环，避免选择到重复元素，达到剪枝的效果） （非常常用！！！）
- 比如在[1,2,3]中，当前的visited为[2,3]. 此时站在节点处，回头一看，已经走过了2和3，因此在面对选择列表时，只选1（通过continue跳过2和3）
利用visited.append(num) 和 visited.pop() 可更新路径（添加/回退选择）
res.append(visited[:]) 利用visited[:] 才可完整复制添加单个排列结果(深拷贝)
- a[:]是深复制，a是浅复制，相当于赋值a的话是赋值了指针，赋值a[:]相当于复制了a对应的那段空间
  - 如果使用for x in a，则在for循环中会改变a的内容；如果使用for x in a[:]，则会建立一个a的副本（新对象），这个副本和a中的内容完全相同，所以我们可以在a已经修改的情况下进行remove操作

class Solution(object):
    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        res=[]
        # visited=[]  # 不用加这一行
        def backtrack(nums,visited):# 选择列表和路径
            if len(visited)==len(nums):
                res.append(visited[:])
                return
            for num in nums:
                if num in visited:
                    continue
                else:
                    visited.append(num)
                    backtrack(nums,visited)
                    visited.pop()
        backtrack(nums,[])
        return res


# 或者分开写
# class Solution(object):
#     def __init__(self):
#         self.res = []

#     def backtrance(self, nums, visited):
#         if len(nums) == len(visited):
#             self.res.append(visited[:])
#             return
#         for i in range(len(nums)):
#             if nums[i] in visited:
#                 continue
#             else:
#                 visited.append(nums[i])
#                 self.backtrance(nums, visited)
#                 visited.pop()

#     def permute(self, nums):
#         """
#         :type nums: List[int]
#         :rtype: List[List[int]]
#         """
#         self.backtrance(nums, [])
#         return self.res

//#include <vector>
//#include <iostream>
//#include <algorithm>
//
//using namespace std;

class Solution {
public:
    vector<vector<int>> res;
    vector<int> visited;

    void backtrack(vector<int> nums, vector<int> visited) {
        if (visited.size() == nums.size()) {
            res.push_back(visited);
            return;
        }

        for (int num :nums) {
//            检查当前num是否在路径中，count返回0（不在）或1（在）
            if (count(visited.begin(), visited.end(), num))
                continue;
            visited.push_back(num);
            backtrack(nums, visited);
            visited.pop_back();
        }
    }

    vector<vector<int>> permute(vector<int> &nums) {
        backtrack(nums, visited);
        return res;
    }
};

//int main() {
//    vector<int> nums = {1, 2, 3};
//    Solution so;
//    vector<vector<int>> output = so.permute(nums);
//
////    结果的两种输出方式：1
//    for (auto out:output) {
//        for (auto each: out) {
//            cout << each;
//        }
//        cout << endl;
//    }
////    结果的两种输出方式：2
//    for (auto it = output.begin(); it <output.end(); ++it) {
//        for (auto j = (*it).begin(); j < (*it).end(); ++j) {
//                cout<<(*j);
//        }
//        cout<<endl;
//    }
//}

78. 子集

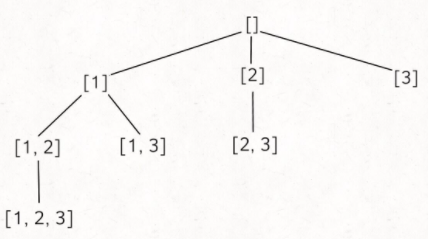
图片来自labuladong

方法1（更容易理解）

要有回溯结束的条件
用nums[i+1:]更新选择列表
for循环中：做选择->回溯->撤销选择

class Solution(object):
    def subsets(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        # nums.sort()
        def backtrack(nums,visited):
            # 回溯结束的条件：nums里没有元素了
            if not nums:
                return
            for i in range(len(nums)):
                # 做选择
                visited.append(nums[i])
                res.append(visited[:])
                # 回溯，用nums[i+1:]更新选择列表
                backtrack(nums[i+1:],visited)
                # 撤销选择
                visited.pop()
        res=[[]]
        backtrack(nums,[])
        return res
# nums=[1,2,3]
# s=Solution()
# print(s.subsets(nums))

c++中，用一个start记录nums开始的地方

//#include <vector>
class Solution {
public:
    void dfs (vector<int>& nums,vector<int> &visited,int start){
        if (nums.empty())
            return;
        for (int i = start; i < nums.size(); ++i) {
            visited.push_back(nums[i]);
            res.push_back(visited);
            //后面的dfs过程，只能选择nums[i+1:]范围的元素
            dfs(nums,visited,i+1);
            visited.pop_back();
        }
    }
//    全局变量保存结果
    vector<vector<int>> res;
    vector<vector<int>> subsets(vector<int>& nums) {

        vector<int> visited;
        res.push_back(visited);
        int start=0;
        dfs(nums,visited,start);
        return res;
    }
};

方法1的另一种写法（供参考）

在深度遍历决策树时，由于每个visited处对应的后续选择不一样，所以在回溯函数中加入idx参数用于记录选择的范围
详细解释：
- 每次传入子递归的 index 是：当前你选的数的索引+1
- 每次递归枚举的选项变少，一直递归到没有可选的数字，进入不了for循环，落入不了递归，整个DFS结束
- 可见我们没有显式地设置递归的出口，而是通过控制循环的起点，使得最后递归自然结束

class Solution(object):
    def subsets(self,nums):
        def backtrack(nums,idx,visited):
            res.append(visited[:])
            for i in range(idx,n):
                visited.append(nums[i])
                backtrack(nums,i+1,visited)
                visited.pop()
        res = []
        visited=[]
        n=len(nums)
        backtrack(nums,0,visited)
        return res

nums=[1,2,3]
s=Solution()
print(s.subsets(nums))
# 结果：[[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]

方法2（纯递归写法）

该题也可以用递归来解决：比如[1,2,3]的子集可以由[1,2]的子集基础上，在各个子集元素上追加3得到

class Solution(object):

    # 直接合并递归的写法
    def subsets(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        res=[[]]
        for i in nums:
            res=res+[ num+[i] for num in res]
        return res

    # 不合并，逐步递归的写法
    def subsets(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        # 递归结束的条件
        if not nums:return [[]]
        # 取出nums的最后一个元素
        n=nums[-1]
        nums.pop()

        # 先计算子集结果
        res=self.subsets(nums)
        # 再在子集的基础上追加
        res+=[i+[n] for i in res]
        return res

# s = Solution()
# nums = [1, 2, 3]
# ans = s.subsets(nums)
# print(ans)

class Solution {
public:
    vector <vector<int>> subsets(vector<int> &nums) {
        // 递归结束的条件
        if (nums.empty()) return {{}};

//        把最后一个元素取出来
        int n = nums.back();
        nums.pop_back();
//        得到子问题的结果
        vector <vector<int>> res = subsets(nums);
//        在结果上依次追加
        int size = res.size();
        for (int i = 0; i < size; i++) {
            res.push_back(res[i]);
            res.back().push_back(n);
        }
        return res;
    }
};

77. 组合

与上一题类似，也是用一个位置参数记录当前节点，然后调用子问题的backtrack时，选择列表从位置参数后面开始

78题子集问题：选择列表为空时跳出，每经过一个节点，记录当前visited路径
本题：visited的路径为给定的k时，结果中记录当前的visited，然后跳出

class Solution(object):
    def combine(self, n, k):
        """
        :type n: int
        :type k: int
        :rtype: List[List[int]]
        """
        nums=[i for i in range(1,n+1)]
        res=[]
        visited=[]
        def backtrance(nums,visited):
            if len(visited)==k:
                res.append(visited[:])
                return
            for i in range(len(nums)):
                visited.append(nums[i])
                backtrance(nums[i+1:],visited)
                visited.pop()
        backtrance(nums,visited)
        return res
# so=Solution()
# print(so.combine(4,2))

class Solution {
public:
//    用start记录选择列表开始的地方，小于该节点的选择一律不选
    void  backtrack(vector<int> nums, vector<int> visited,int start,int k){
        if (visited.size()==k){
            res.push_back(visited);
            return ;
        }

        for (int j = start; j < nums.size(); ++j) {
            visited.push_back(nums[j]);
            backtrack(nums,visited,j+1,k); // 从位置j后面的列表中选
            visited.pop_back();
        }

    }

    vector<vector<int>>res;
    vector<int> visited;
    vector<vector<int>> combine(int n, int k) {
        //    构建1到n的向量
        vector<int> nums;
        for(int i=1;i<n+1;i++){
            nums.push_back(i);
        }
        int start = 0;
        backtrack(nums,visited,start,k);
        return res;
    }
};

17. 电话号码的字母组合

方法1：回溯

用一个dic记录按键对应的字母
维护选择列表choice和已选择的路径visited
用idx记录digits当前索引的位置,不同的idx对应不同的选择
- 在函数参数列表中用idx记录索引这种操作很常见，相当于用idx更新选择列表

class Solution(object):
    def letterCombinations(self, digits):
        """
        :type digits: str
        :rtype: List[str]
        """
        # dic = {"2": ['a', 'b', 'c'],
        #        "3": ['d', 'e', 'f'],
        #        "4": ['g', 'h', 'i'],
        #        "5": ['j', 'k', 'l'],
        #        "6": ['m', 'n', 'o'],
        #        "7": ['p', 'q', 'r', 's'],
        #        "8": ['t', 'u', 'v'],
        #        "9": ['w', 'x', 'y', 'z']}
        dic = {
            '2': 'abc',
            '3': 'def',
            '4': 'ghi',
            '5': 'jkl',
            '6': 'mno',
            '7': 'pqrs',
            '8': 'tuv',
            '9': 'wxyz'
        }

        def backtrace(digits,visited, idx):
            if len(visited) == len(digits): # 回溯结束的条件
                res.append(visited)
                return

            # 维护路径和选择列表
            choose = dic[digits[idx]]# 按照索引 选择 选择列表
            for i in range(len(choose)):
                visited+=choose[i]  # 选择
                backtrace(digits,visited, idx + 1)
                visited=visited[:-1] # 撤销选择


        if digits=="":return []
        visited=""
        res = []
        backtrace(digits, visited,0)
        return res


# so = Solution()
# print(so.letterCombinations("23"))

// #include <string>
// #include <vector>
// #include <map>
// #include <iostream>
// #include <unordered_map>
// using namespace std;

class Solution {
public:
    vector<string> ans;
    unordered_map<char, string> table{
            {'0', " "},
            {'1', "*"},
            {'2', "abc"},
            {'3', "def"},
            {'4', "ghi"},
            {'5', "jkl"},
            {'6', "mno"},
            {'7', "pqrs"},
            {'8', "tuv"},
            {'9', "wxyz"}};

    void backtrack(string digits,string visited,int idx) {
//        递归结束的条件，
        if (idx==digits.size()) { // 或者 if (visited.size()==digits.size())...
            ans.push_back(visited);
            return;
        }

        string choice = table[digits[idx]];// 当前的选择列表
        for (auto &i:choice) {
            visited.push_back(i); // 做选择
            backtrack(digits,visited,idx+1); // 递归
            visited.pop_back(); // 撤销选择
        }
    }

    vector<string> letterCombinations(string digits) {
        // 输入：digits = ""，输出：[] （而不是[""]）,所以加这句话进行特判
        if(digits == "") return ans;
        backtrack(digits,"",0);
        return ans;
    }
};
// int main() {
//     Solution s;
//     string digits = "23";
//     vector<string> res = s.letterCombinations(digits);
//     for (auto &i:res) {
//         cout << i << '\t';
//     }
// }

方法2：纯递归

用当前按键对应的内容和递归返回的结果进行拼接，得到最终结果

明确递归函数的含义（不要跳进递归中）：返回digits对应的题目要求的结果
- 选择第一个按键作为当前列表，然后把当前列表和子结果进行拼接，得到最终结果
- 注意递归结束的条件：digits长度为0，则…; digits长度为1，则… (有时候不确定递归结束的条件，则可以多写些base case)

class Solution(object):
    def letterCombinations(self, digits) :
        if not digits:
            return []
        dict = {
            '2': 'abc',
            '3': 'def',
            '4': 'ghi',
            '5': 'jkl',
            '6': 'mno',
            '7': 'pqrs',
            '8': 'tuv',
            '9': 'wxyz'
        }

        # res = [] # 注意：res一定不要写在这里，否则递归过程中，res不断增加，导致出错
        def recursive(digits):
            # 递归结束的条件
            if len(digits)==0:
                return []
            if len(digits)==1:
                return list(dict[digits[0]]) # 注意，这也是递归结束的条件

            children = dict[digits[0]] # 选择当前按键对应的列表
            digits=digits[1:]
            res=[]  # res写在这里，递归过程中，不断填充并更新res
            for child in children:
                subRes=recursive(digits) # 子结果
                for i in subRes: # 拼接结果并记录
                    tmp=child+i
                    res.append(tmp)
            return res
        return recursive(digits)

# so=Solution()
# print(so.letterCombinations("234"))


## 或者
class Solution(object):
    def letterCombinations(self, digits) :
        if not digits:
            return []
        dict = {
            '2': 'abc',
            '3': 'def',
            '4': 'ghi',
            '5': 'jkl',
            '6': 'mno',
            '7': 'pqrs',
            '8': 'tuv',
            '9': 'wxyz'
        }

        def recursive(digits):
            if len(digits)==0:
                return []
            if len(digits)==1:
                return list(dict[digits[0]])
            children = dict[digits[-1]]
            digits=digits[:-1]
            res=[]
            subRes=recursive(digits)
            for i in subRes:
                for child in children:
                    tmp=i+child
                    res.append(tmp)
            return res
        return recursive(digits)

# so=Solution()
# print(so.letterCombinations("234"))

其他写法：

明确递归函数的含义recursive(digits, visited)：给定digits以及已经选择的路径，返回题目要求的结果。注意：不要跳进递归中
递归结束的条件：digits的长度为0

class Solution(object):
    def letterCombinations(self, digits) :


        dict = {
            '2': 'abc',
            '3': 'def',
            '4': 'ghi',
            '5': 'jkl',
            '6': 'mno',
            '7': 'pqrs',
            '8': 'tuv',
            '9': 'wxyz'
        }


        if not digits:
            return []
        res=[]
        def recursive(digits, visited):
            # 递归结束的条件
            if len(digits)==0:
                res.append(visited)
                return 
            children = dict[digits[0]] # 选择当前数字对应的字母按键串
            for child in children:
                recursive(digits[1:], visited+child) # 根据字母按键串中的字符更新visted
            return res
        return recursive(digits, "")


# so=Solution()
# print(so.letterCombinations("23"))

C++的其他写法：

用递归得到前面的结果，然后把前面的结果与当前的字符串进行拼接

递归结束的条件是digits.size() == 0则返回{""}。这样在递归树的最低层是从""开始的，而不是从a（或b或c）开始，所以结果中记录的是全部的按键过程，最后要用长度过滤结果

// #include <string>
// #include <vector>
// #include <map>
// #include <iostream>
// #include <unordered_map>
// #include<algorithm>

// using namespace std;

class Solution {
public:
    unordered_map<char, string> table{
            {'0', " "},
            {'1', "*"},
            {'2', "abc"},
            {'3', "def"},
            {'4', "ghi"},
            {'5', "jkl"},
            {'6', "mno"},
            {'7', "pqrs"},
            {'8', "tuv"},
            {'9', "wxyz"}};
    vector<string> ans;

    vector<string> helper(string &digits) {
        if (digits.size() == 0) {
            return {""};
        } // 递归结束的条件
        string cur = table[digits.back()];
        digits.pop_back(); // 取出最后一个元素
        vector<string> subRes = helper(digits); // 前面的结果
        for (auto &i :subRes) { // 前面的结果与当前元素进行拼接
            for (auto &j:cur) {
                string tmp = i + j;
                ans.push_back(tmp);
            }
        }
        return ans;
    }

    vector<string> letterCombinations(string digits) {
        if(digits == "") return ans; // 特判
        int n = digits.size();
        vector<string> output = helper(digits);
        vector<string> ans1;
        for (auto &i:output){ // 过滤掉不满足长度数的字符串
            if (i.size() == n){
                ans1.push_back(i);
            }
        }
        return ans1;

    }
};
// int main() {
//     Solution s;
//     string digits = "23";
//     vector<string>res=s.letterCombinations(digits);
//     for (auto &i:res) {
//         cout << i << '\t';
//     }
// }

51. N皇后

与全排列类似，决策树的每一层表示棋盘上的每一行；每个节点可以做出的选择是，在该行的任意一列放置一个皇后。
backtrack(board,row) 就是标准的回溯框架，只是在做选择时，通过isvalid() 函数进行剪枝（continue 跳出当次循环），得到符合条件的排列
- isvalid() 函数检查当列，左上，右上是否与皇后有冲突
- tmp_res.append(''.join(b)) 的作用是得到符合输出格式的皇后摆放

class Solution(object):
    def solveNQueens(self, n):
        board=[['.' for _ in range(n)] for _ in range(n)]
        res=[]
        # 路径：board, 选择列表：row中的每一列
        def backtrack(board,row):
            #     if 满足条件:
            #         res.append(路径)
            #         return
            # 触底，添加
            if row==n:
                tmp_res=[]
                for b in board:
                    tmp_res.append(''.join(b))
                res.append(tmp_res)
                return res

            #     for 选择 in 选择列表:
            #         做选择
            #         backtrack(路径,选择列表)
            #         撤销选择
            # 判断row行，col列是否可以放Q
            for col in range(n):
                if not isvalid(row,col):
                    continue
                board[row][col]='Q'
                backtrack(board,row+1)
                board[row][col]='.'


        def isvalid(row,col):
            # 检查列是否有皇后互相冲突
            for i in range(row):
                if board[i][col]=='Q':
                    return False

            # 检查左上方是否有皇后互相冲突
            l_row,l_col=row,col
            while 0<=(l_row-1)<n and 0<=(l_col-1)<n:
                l_row-=1
                l_col-=1
                if board[l_row][l_col]=='Q':
                    return False

            # 检查右上方是否有皇后互相冲突
            r_row,r_col=row,col
            while 0<=(r_row-1)<n and 0<=(r_col+1)<n:
                r_row-=1
                r_col+=1
                if board[r_row][r_col]=='Q':
                    return False
            return True
        backtrack(board, 0)
        return res