动手学深度学学习_pytorch版

《动手学深度学习》(Pytorch版)

• github 中有每章节的code源文件，clone到本地运行，可观察各模型效果。

---

3.4.5 交叉熵损失函数

交叉熵只关心对正确类别的预测概率，因为只要其值足够大，就可以确保分类结果正确

交叉熵损失（Cross Entropy Loss）计算过程

3.5.1 获取数据集

transform = transforms.ToTensor()使所有数据转换为Tensor，如果不进行转换则返回的是PIL图片。transforms.ToTensor()将尺寸为(H x W x C)且数据位于[0, 255]的PIL图片或者数据类型为np.uint8的NumPy数组转换为尺寸为(C x H x W)且数据类型为torch.float32且位于[0.0, 1.0]的Tensor。

3.8 多层感知机

上述问题的根源在于全连接层只是对数据做仿射变换（affine transformation），而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换，例如对隐藏变量使用按元素运算的非线性函数进行变换，然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数（activation function）。

3.12 权重衰减

• 正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小，是应对过拟合的常用手段。
• 权重衰减等价于L2范数正则化，通常会使学到的权重参数的元素较接近0。
• 权重衰减可以通过优化器中的weight_decay超参数来指定。
• 可以定义多个优化器实例对不同的模型参数使用不同的迭代方法。

经典CNN结构简析：AlexNet、VGG、NIN、GoogLeNet、ResNet etc

5.5.1 LeNet模型

以单通道的28*28图片为例，各层网络输入输出说明如下：

import time
import torch
from torch import nn, optim

import sys
sys.path.append("..") 
import d2lzh_pytorch as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size.  1@28*28  ->  6@*(28-5+1)*(28-5+1)
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2), # kernel_size, stride. 6@24*24->6@12*12
            nn.Conv2d(6, 16, 5),  # 6@12*12  ->  16@(12-5+1)*(12-5+1)
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2) # 16*8*8  ->   16@4*4
        )
        self.fc = nn.Sequential(
            nn.Linear(16*4*4, 120), # 把16张4*4的图片拉平（该向量长度为通道*高*宽），全连接层输入为16*4*4，输出为120
            nn.Sigmoid(),
            nn.Linear(120, 84), # 同上
            nn.Sigmoid(),
            nn.Linear(84, 10)   # 同上
        )

    def forward(self, img):
        feature = self.conv(img)
        output = self.fc(feature.view(img.shape[0], -1)) # 通过view，把特征变成 batch_size 行，通道数*高*宽  列
        return output

CNN卷积神经网络特征可视化: 二维， 三维

5.7 使用重复元素的网络（VGG）

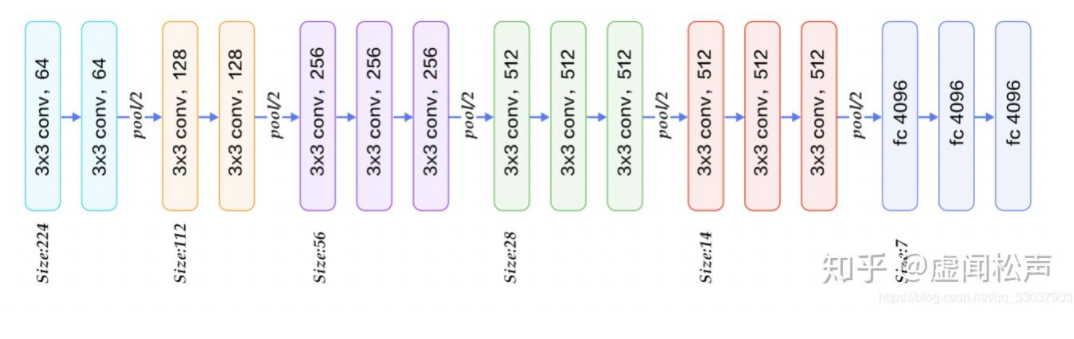
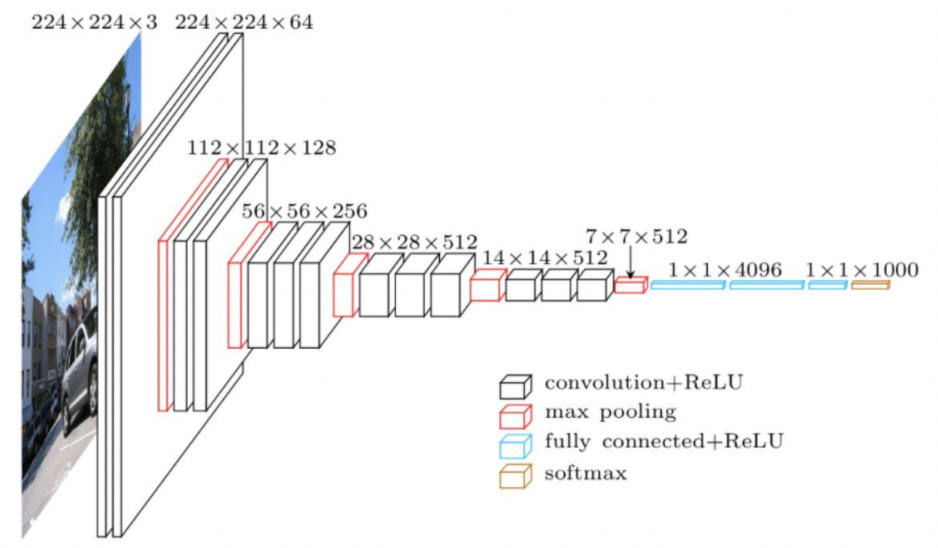
• VGG块的组成规律是：使用的卷积全部为3x3，Pad=1，步长为1，也就是说，卷积不会改变输出大小（假设2828的图片，），而改变输出大小这件事就交给了2x2，步长为2 的max pool，也就是说每通过一个 max pool，卷积的尺寸都会折半。*卷积层保持输入的高和宽不变，而池化层则对其减半。
• VGG这种高和宽减半以及通道翻倍的设计使得多数卷积层都有相同的模型参数尺寸和计算复杂度。

对于给定的感受野（与输出有关的输入图片的局部大小），采用堆积的小卷积核优于采用大的卷积核，因为可以增加网络深度来保证学习更复杂的模式，而且代价还比较小（参数更少）。例如，在VGG中，使用了3个3x3卷积核来代替7x7卷积核，使用了2个3x3卷积核来代替5*5卷积核，这样做的主要目的是在保证具有相同感知野的条件下，提升了网络的深度，在一定程度上提升了神经网络的效果。

图片来源：VGG网络结构详解