SLAM

计算机基础

发布日期: 2021-06-12

作者: M

文章字数: 8k

阅读时长: 29 分

热度:

视频讲解
 第一版配套代码
 第二版配套代码（prefer）

高翔：视觉slam是什么？
坐标系，三角测量，PNP
EPNP算法原理

库说明：

Eigen：几何模块
Sophus：李代数模块（在Eigen基础上开发）
优化库
- Ceres 库面向通用的最小二乘问题的求解，作为用户，我们需要做的就是定义优化问题，然后设置一些选项，输入进 Ceres 求解即可
- g2o是一个基于图优化的库（General Graphic Optimization）。为了使用 g2o，首先要做的是将问题抽象成图优化。这个过程中，只要记住节点为优化变量，边为误差项即可

第二讲

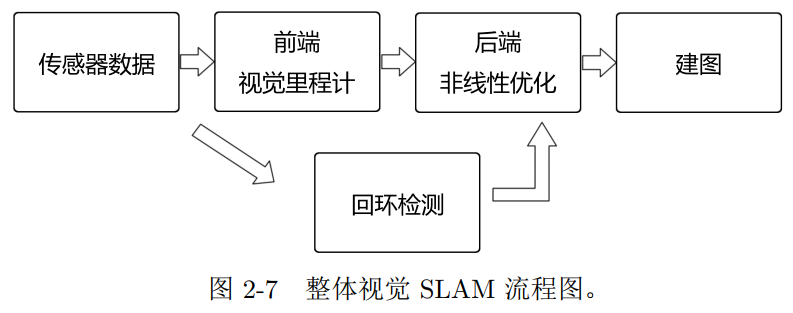
我们把整个视觉 SLAM 流程分为以下几步：

传感器信息读取。在视觉 SLAM 中主要为相机图像信息的读取和预处理。如果在机
器人中，还可能有码盘、惯性传感器等信息的读取和同步。
视觉里程计 (Visual Odometry, VO)。视觉里程计任务是估算相邻图像间相机的运动，
以及局部地图的样子。 VO 又称为前端（Front End）。
- 视觉里程计关心相邻图像之间的相机运动，最简单的情况当然是两张图像之间的运动
  关系
后端优化（Optimization）。后端接受不同时刻视觉里程计测量的相机位姿，以及回
环检测的信息，对它们进行优化，得到全局一致的轨迹和地图。由于接在 VO 之后，
又称为后端（Back End）。
- 笼统地说，后端优化主要指处理 SLAM 过程中噪声的问题。后端优化要考虑的问题，
  就是如何从这些带有噪声的数据中，估计整个系统的状态，以及这个状态估计的不确定性
  有多大——这称为最大后验概率估计（Maximum-a-Posteriori， MAP）。这里的状态既包括
  机器人自身的轨迹，也包含地图
  
  在视觉 SLAM 中，前端和计算机视觉研究领域更为相关，比如图像的特征提取与匹配等，后端则主要是滤波与非线性优化算法。
回环检测（Loop Closing）。回环检测判断机器人是否曾经到达过先前的位置。如果
检测到回环，它会把信息提供给后端进行处理。
建图（Mapping）。它根据估计的轨迹，建立与任务要求对应的地图

使用库

新建一个项目，名称为P1
在P1中新建一个类，名称为libSLAM
- 在libSLAM.h 中，声明printSLAM函数

```cpp
#ifndef P1_LIBSLAM_H
#define P1_LIBSLAM_H


class libSLAM {
public:
    void printSLAM();
};

#endif //P1_LIBSLAM_H
```

在libSLAM.cpp 中，实现printSLAM函数

#include "libSLAM.h"
#include <iostream>
using namespace  std;

void libSLAM::printSLAM(){
    cout<<"Hello SLAM"<<endl;
}

在main文件的main函数（可以为任意文件名称中的任意函数，不一定为main）中，调用printSLAM

#include "libSLAM.h"

int main() {
  libSLAM l;
  l.printSLAM();
  return 0;
}

修改cMakeLists文件的内容

cmake_minimum_required(VERSION 3.19)
project(P1)

set(CMAKE_CXX_STANDARD 14)

# 通过main.cpp生成可执行文件main
add_executable(main main.cpp)
# 通过libSLAM.cpp 生成库文件useLib
add_library(useLib libSLAM.cpp)
# 将可执行文件main链接到useLib静态库文件中
target_link_libraries(main useLib)

其中，库文件分为静态库（以.a为后缀）和共享库（以.so为后缀）。静态库每次被调用都会生成一个副本，而共享库则只有一个副本，更省空间。cMakeLists中可以分别写为：

# (静态库)
# 通过libSLAM.cpp 生成库文件useLib
add_library(useLib libSLAM.cpp)
# 将可执行文件main链接到useLib静态库文件中
target_link_libraries(main useLib)
# （共享库）
# 如果想生成共享库，则使用关键字 SHARED：
add_library(useLib_Shared SHARED libSLAM.cpp)    
# 将共享库文件useLib_Shared链接到可执行文件main中
target_link_libraries(main useLib_Shared)

如果只有头文件（e.g., Eigen库只有头文件），则不需要用target_link_libraries将程序链接到库上，但需要在cMakeLists中添加include_directories("/usr/include/eigen3/")
- （也可以写成include_directories(${/usr/include/eigen3/})）
- （可通过locate eigen3查找相应位置）
- 可以把头文件写到文件夹下，然后在CMakeLists.txt 中将其添加进去。比如在当前文件夹->includes->math文件夹（该文件夹中有一个头文件header_math.h），则CMakeLists.txt中添加include_directories (includes/math)即可

find_package命令是cmake提供的寻找某个库的头文件与库文件的指令。如果 cmake能够找到它，就会提供头文件和库文件所在的目录的变量 (参考该链接)。在 Sophus 这个例子中，就是Sophus_INCLUDE_DIRS 和 Sophus_LIBRARIES 这两个变量。根据它们，我们就能将Sophus 库引入自己的 cmake 工程了：

  # 为使用 sophus ，需要使用 find_package 命令找到它
  find_package( Sophus REQUIRED )
  # 将头文件包含进去,  也可以写成 include_directories( "Sophus_INCLUDE_DIRS" )  
  include_directories( ${Sophus_INCLUDE_DIRS} )  

  add_executable( useSophus useSophus.cpp )  # useSophus 为主文件生成的执行文件 （类似于main.cpp的地位）
  target_link_libraries( useSophus Sophus::Sophus) # 将库文件上链接到执行文件中

Quick CMake tutorial及配套代码

CMakeLists.txt示例1

cmake_minimum_required(VERSION 2.8)
project(vo1)

set(CMAKE_BUILD_TYPE "Release")
add_definitions("-DENABLE_SSE")
set(CMAKE_CXX_FLAGS "-std=c++11 -O2 ${SSE_FLAGS} -msse4")
list(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake)

find_package(OpenCV 3 REQUIRED)
find_package(G2O REQUIRED)
find_package(Sophus REQUIRED)

include_directories(
        ${OpenCV_INCLUDE_DIRS}
        ${G2O_INCLUDE_DIRS}
        ${Sophus_INCLUDE_DIRS}
        "/usr/include/eigen3/"
)

add_executable(orb_cv orb_cv.cpp)
target_link_libraries(orb_cv ${OpenCV_LIBS})

add_executable(orb_self orb_self.cpp)
target_link_libraries(orb_self ${OpenCV_LIBS})

# add_executable( pose_estimation_2d2d pose_estimation_2d2d.cpp extra.cpp ) # use this if in OpenCV2
add_executable(pose_estimation_2d2d pose_estimation_2d2d.cpp)
target_link_libraries(pose_estimation_2d2d ${OpenCV_LIBS})

# # add_executable( triangulation triangulation.cpp extra.cpp) # use this if in opencv2
add_executable(triangulation triangulation.cpp)
target_link_libraries(triangulation ${OpenCV_LIBS})

add_executable(pose_estimation_3d2d pose_estimation_3d2d.cpp)
target_link_libraries(pose_estimation_3d2d
        g2o_core g2o_stuff
        ${OpenCV_LIBS})

add_executable(pose_estimation_3d3d pose_estimation_3d3d.cpp)
target_link_libraries(pose_estimation_3d3d
        g2o_core g2o_stuff
        ${OpenCV_LIBS})

CMakeLists.txt示例2

20210808152734

cmake_minimum_required(VERSION 3.19)
project(P1)

set(CMAKE_CXX_STANDARD 14)

#先建立两个可执行文件
add_executable(P1 main.cpp)
add_executable(P1_calc main.cpp calc.cpp)

#从calc.cpp中构建并增加静态库 （添加共享库的方式同理，关键词为SHARED）
add_library(stat_lib STATIC calc.cpp)
#将静态库连接到可执行文件中
find_library(SLIB stat_lib lib)
target_link_libraries(P1 LINK_PUBLIC ${SLIB})

# 添加自建的头文件库
include_directories(includes/general)

# 添加第三方的头文件或库文件，如OpenCV，Sophus等
# 为使用 sophus ，需要使用 find_package 命令找到它
find_package( Sophus REQUIRED )
# 将头文件包含进去,  也可以写成 include_directories( "Sophus_INCLUDE_DIRS" )
include_directories( ${Sophus_INCLUDE_DIRS} )
# 将库文件包含进去
add_executable(P1 main.cpp)
target_link_libraries(P1 Sophus::Sophus) # 将库文件上链接到执行文件中

第三讲

内积和外积

向量内积外积的计算以及几何意义
- 内积的结果为一个数
- 内积（点乘）的几何意义包括：
  - 表征或计算两个向量之间的夹角
  - b向量在a向量方向上的投影
- 外积的结果为一个垂直于a，b向量所在平面的向量（法向量方向）。大小为|a||b|sin<a,b>,是两个向量张成的四边形的有向面积
Eigen中几乎所有的数据都当做矩阵来处理。为使效率更高，需要指定矩阵的大小和类型

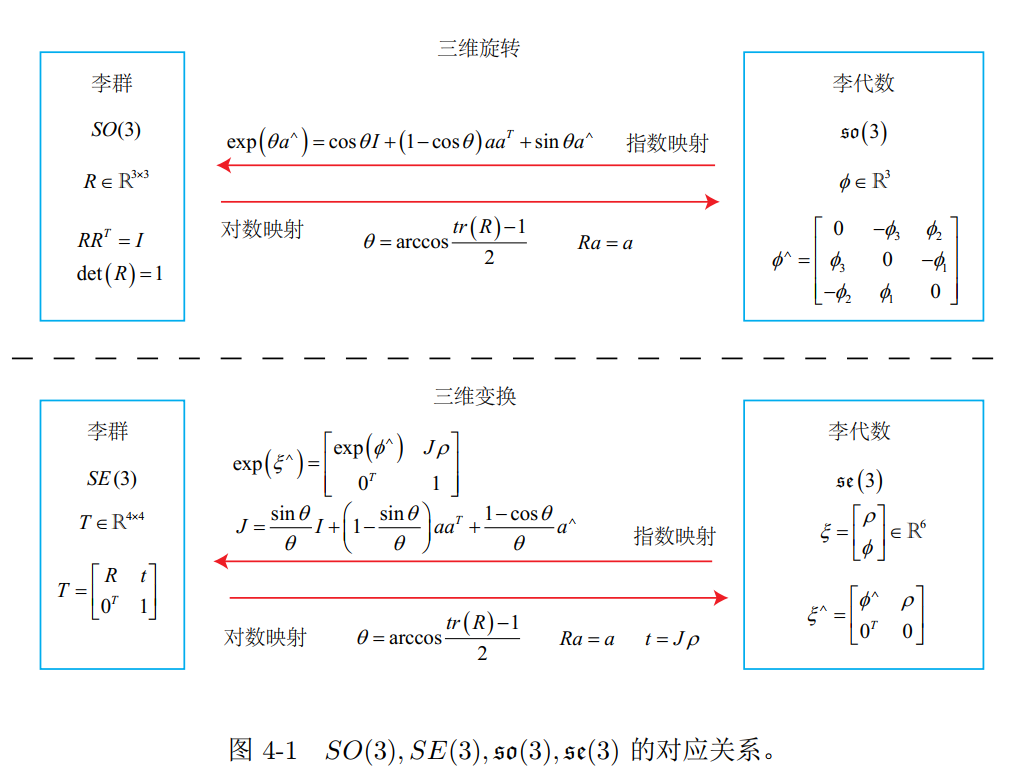
SO（n）和SE（n）

so（n）是特殊正交群，这个集合由n维旋转空间矩阵组成
坐标系之间的运动由欧氏变换描述，它由平移和旋转组成。旋转可以由旋转矩阵 SO(3)描述，而平移直接由一个 R^3 向量描述。最后，如果将平移和旋转放在一个矩阵中，就形成了变换矩阵 SE(3)。

旋转向量（不紧凑）

由于上述的旋转矩阵和变换矩阵相对冗余，需要用更紧凑的方式表达旋转：旋转向量。而旋转向量和旋转矩阵之间可以相互转换

在对坐标系进行变换时，需要经过旋转和平移
任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是，我们可以使用一个向量，其方向与旋转轴一致，而长度等于旋转角。这种向量，称为旋转向量（或轴角， AxisAngle）。这种表示法只需一个三维向量即可描述旋转。同样，对于变换矩阵，我们使用一个旋转向量和一个平移向量即可表达一次变换。这时的维数正好是六维（事实上，旋转向量就是我们下章准备介绍的李代数）

欧拉角（有奇异性）

旋转向量和旋转角相对人类而言并不直观。而欧拉角提供了3个分离的转角来描述旋转，相对直观一些，但会陷入万向锁问题，使得系统丢失了一个自由度（由三次旋转变成了两次旋转），所以也很少在SLAM中直接使用欧拉角

四元数（既紧凑，又没有奇异性）

一个四元数有一个实部和三个虚部。用四元数可以表示旋转
四元数可以与旋转向量、旋转矩阵之间进行转换

代码调试

plotTrajectory.cpp
- 添加集合模块头文件#include <Eigen/Geometry>
- 将文件路径./examples/trajectory.txt改为../../examples/trajectory.txt
visualizeGeometry
- 若报错，重新编译一次pangolin即可

第四讲

李群和李代数

给定某时刻的旋转矩阵R，我们就能求得一个 ϕ，它描述了 R 在局部的导数关系。与 R 对应的 ϕ 有什么含义呢？我们说， ϕ 正是对应到 SO(3) 上的李代数 so(3)，也就是说，李代数描述了李群的局部性质；
其次，给定某个向量ϕ时，矩阵指数 exp(ϕ^) 如何计算？反之，给定R时，能否有相反的运算来计算ϕ？——事实上，这正是李群与李代数间的指数/对数映射

李群 -> 一些矩阵的集合

三维旋转矩阵构成了特殊正交群 SO(3)，而变换矩阵构成了特殊欧氏群 SE(3)：

群（Group）是一种集合加上一种运算的代数结构。我们把集合记作 A，运算记作 ·，那么群可以记作G = (A; ·)。

李群是指具有连续（光滑）性质的群。像整数群 Z 那样离散的群没有连续性质，所以不是李群。而 SO(n) 和SE(n)，它们在实数空间上是连续的。我们能够直观地想象一个刚体能够连续地在空间中运动，所以它们都是李群

每个李群都有与之对应的李代数。李代数描述了李群的局部性质,准确地说，是单位元附近的正切空间

李代数so（3）和李代数 se（3） -> 一些向量组成的集合

so（3）实际上就是由所谓的旋转向量组成的空间
se（3）

李代数求导和扰动模型

BCH公式
扰动

李群可通过对数映射获得它的李代数（Sophus的使用可参考本书代码slambook2/ch4/useSophus.cpp）

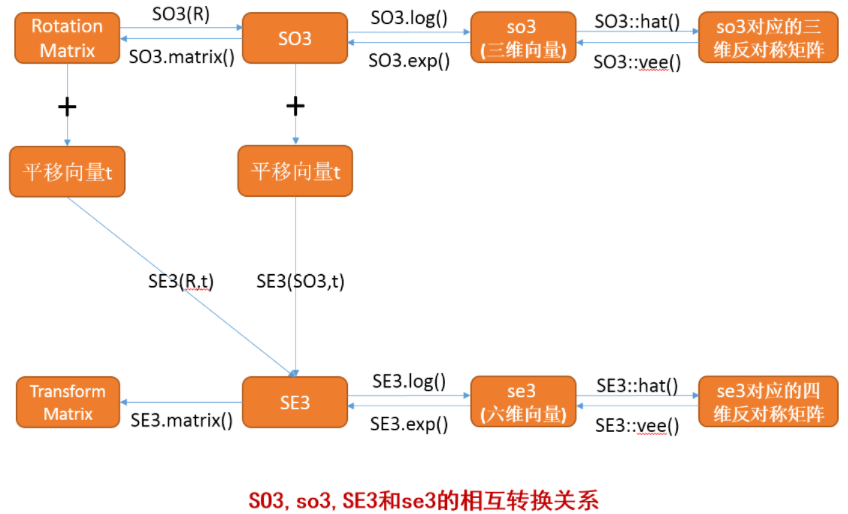
旋转矩阵（R），旋转向量（V）和四元数（Q）在Eigen中转换关系

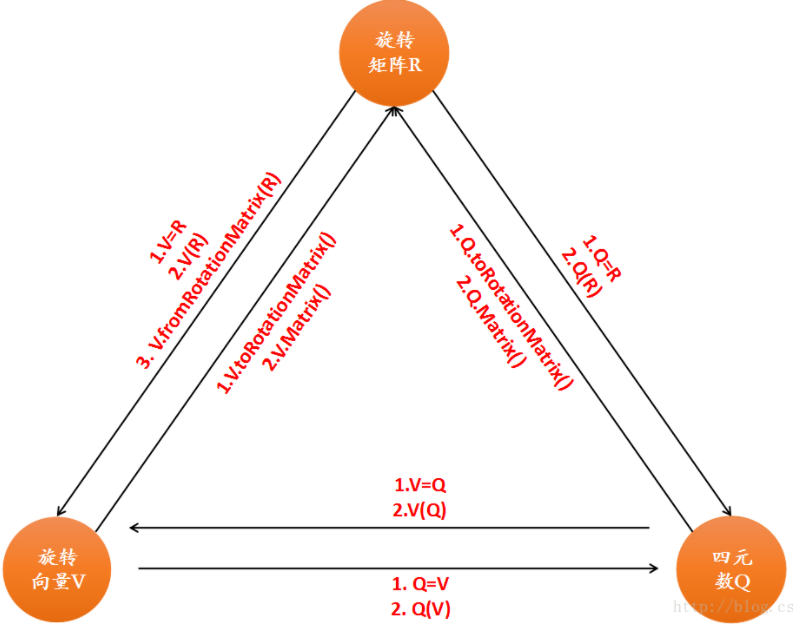
20210728171757

第五讲

Ubuntu 20.04下安装opencv3
根据 RGB-D 图像和相机内参，我们可以计算任何一个像素在相机坐标系下的位置。同时，根据相机位姿，又能计算这些像素在世界坐标系下的位置。如果把所有像素的空间坐标都求出来，相当于构建一张类似于地图的东西
若有多张RGB-D图像，且知道每个图像的内参（如随相机固定的参数）和外参（如相机位姿信息），则通过求出所有像素的空间信息后，可实现点云拼接
相机内参在出厂后即固定。有些厂商会告诉内参，若没告诉，用标定法即可（已非常成熟）
- 内参的推导可参考5.1.1小节，内参数矩阵中一般包含f_x,f_y （像素）、 c_x,c_y （原点平移）
相机的外参：位姿R,t （旋转矩阵和平移向量）

第六讲

大多现代视觉 SLAM 算法都不需要那么高成本的传感器，甚至也不需要那么昂贵的处理器来计算这些数据，这全是算法的功劳。由于在 SLAM 问题中，同一个点往往会被一个相机在不同的时间内多次观测，同一个相机在每个时刻观测到的点也不止一个。这些因素交织在一起，使我们拥有了更多的约束，最终能够较好地从噪声数据中恢复出我们需要的东西
SLAM中经常会碰到一些非线性优化问题：由许多个误差项平方和组成的最小二乘问题。在优化该问题时，有两种主要的梯度下降方式：Gauss-Newton 和 Levenberg-Marquardt
- 在做最优化计算时，需要提供变量的初始值（在视觉SLAM中，可用ICP，PnP等方法提供优化初始值）
优化库
- 有两个常用的优化库：google的Ceres库和基于图优化的g2o（General Graphic Optimization， G2O）库
  - Ceres 库面向通用的最小二乘问题的求解，作为用户，我们需要做的就是定义优化问题，然后设置一些选项，输入进 Ceres 求解即可
  - 另一个（主要在 SLAM 领域）广为使用的优化库 g2o是一个基于图优化的库。为了使用 g2o，首先要做的是将问题抽象成图优化。这个过程中，只要记住节点为优化变量，边为误差项即可

第七讲

特征点

（基于特征点方式的视觉里程计计算法）

特征点：在视觉里程计中，我们希望特征点在相机运动之后仍保持稳定。（如著名的 SIFT, SURF,ORB等）
- 特征点由关键点（Key-point）和描述子（Descriptor）两部分组成。（比方说，当我们
  谈论 SIFT 特征时，是指“提取 SIFT 关键点，并计算 SIFT 描述子”两件事情）。关键点是指该特征点在图像里的位置，有些特征点还具有朝向、大小等信息。描述子通常是一个向量，按照某种人为设计的方式，描述了该关键点周围像素的信息。描述子是按照“外观
  相似的特征应该有相似的描述子”的原则设计的
  - SIFT特征点：SIFT（尺度不变特征变换， Scale-Invariant Feature Transform）当属最为经典的一种。它充分考虑了在图像变换过程中出现的光照，尺度，旋转等变化，但随之而来的是极大的计算量。由于整个 SLAM 过程中，图像特征的提取与匹配仅仅是诸多环节中的一个，所以在 SLAM 中我们_甚少使用_这种“奢侈”的图像特征
  - FAST关键点： FAST 关键点属于计算特别快的一种特征点（注意这里“关键点”的用词，说明它_没有描述子_）
  - ORB（Oriented FAST and Rotated BRIEF）特征点：ORB特征则是目前看来非常具有代表性的实时图像特征。它改进了FAST 检测子不具有方向性的问题，并采用速度极快的二进制描述子BRIEF，使整个图像特征提取的环节大大加速。提取 ORB 特征分为两个步骤：
    1. FAST 角点提取：找出图像中的” 角点”。相较于原版的 FAST, ORB 中计算了特征点的主方向，为后续的 BRIEF 描述子增加了旋转不变特性。
      - 针对 FAST 角点不具有方向性和尺度的弱点， ORB 添加了尺度和旋转的描述。尺度不变性由构建图像金字塔，并在金字塔的每一层上检测角点来实现。而特征的旋转是由灰度质心法（Intensity Centroid）实现的
    2. BRIEF 描述子：对前一步提取出特征点的周围图像区域进行描述
      - BRIEF 是一种二进制描述子，它的描述向量由许多个 0 和 1 组成，这里的 0 和 1 编码了关键点附近两个像素（比如说 p 和 q）的大小关系：如果 p 比 q 大，则取 1，反之就取 0 （如果我们取了 128 个这样的 p; q，最后就得到 128 维由 0， 1 组成的向量。那么， p和 q 如何选取呢？在作者原始的论文中给出了若干种挑选方法，大体上都是按照某种概率分布，随机地挑选 p 和 q 的位置。 BRIEF 使用了随机选点的比较，速度非常快，而且由于使用了二进制表达，存储起来也十分方便，适用于实时的图像匹配。）
      - 原始的 BRIEF 描述子不具有旋转不变性的，因此在图像发生旋转时容易丢失。而 ORB 在 FAST 特征点提取阶段计算了关键点的方向，所以可以利用方向信息，计算了旋转之后的“Steer BRIEF”特征，使 ORB 的描述子具有较好的旋转不变性
      由于考虑到了旋转和缩放，使得 ORB 在平移、旋转、缩放的变换下仍有良好的表现。同时， FAST 和 BRIEF 的组合也非常的高效，使得 ORB 特征在实时 SLAM 中非常受欢迎
在提取特征点后，接下来，我们希望根据匹配的点对，估计相机的运动。这里由于相机的原理不同，情况发生了变化：
1. 当相机为单目时，我们只知道 2D 的像素坐标，因而问题是根据两组 2D 点估计运动。该问题用对极几何来解决
2. 当相机为双目、 RGB-D 时，或者我们通过某种方法得到了距离信息，那问题就是根据两组 3D 点估计运动。该问题通常用 ICP 来解决
3. 如果我们有 3D 点和它们在相机的投影位置，也能估计相机的运动。该问题通过PnP求解

2D-2D：对极几何（7.3节，单目相机）

需要>=8个点对
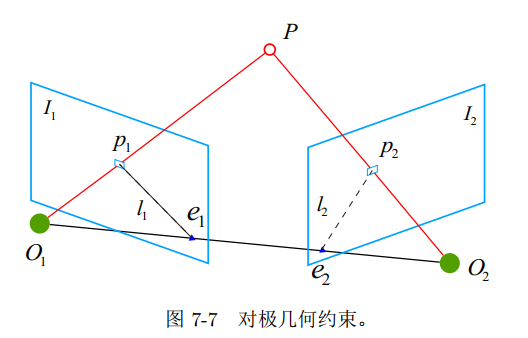
基础矩阵F和本质矩阵E
- 对极约束简洁地给出了两个匹配点的空间位置关系。于是，相机位姿估计问题变为以下两步：
  1. 根据配对点的像素位置，求出 E 或者 F
  2. 根据 E 或者 F，求出 R; t
  - 由于 E 和 F 只相差了相机内参，而内参在 SLAM 中通常是已知的，所以实践当中往往使用形式更简单的 E。
单应矩阵H
- 除了基本矩阵和本质矩阵，我们还有一种称为单应矩阵（Homography） H 的东西，它描述了两个平面之间的映射关系。若场景中的特征点都落在同一平面上（比如墙，地面等），7.3 2D-2D: 对极几何则可以通过单应性来进行运动估计。这种情况在无人机携带的俯视相机，或扫地机携带的顶视相机中比较常见
- 单应性在 SLAM 中具重要意义。当特征点共面，或者相机发生纯旋转的时候，基础矩阵的自由度下降，这就出现了所谓的退化（degenerate）。现实中的数据总包含一些噪声，这时候如果我们继续使用八点法求解基础矩阵，基础矩阵多余出来的自由度将会主要由噪声决定。为了能够避免退化现象造成的影响，通常我们会同时估计基础矩阵 F 和单应矩阵H，选择重投影误差比较小的那个作为最终的运动估计矩阵
在经过特征点匹配后，slambook2/ch7/pose_estimation_2d2d.cpp 文件使用匹配好的特征点来计算本质矩阵E; F 和 H，进而分解 E 得相机的位姿R; t。（从 E; F 和 H 都可以分解出运动，不过 H 需要假设特征点位于平面上，（而本实验特征点不在同一平面），所以我们这里主要用E 来分解运动。）
在单目SLAM中，仅通过单张图像无法获得像素的深度信息，但有多张图像时，可通过三角测量的方法获得像素深度slambook/ch7/triangulation.cpp
- 在增大平移，会导致匹配失效；而平移太小，则三角化精度不够——这就是三角化的矛盾

3D-2D：PnP （7.7节,双目或 RGB-D 相机）

需要>=3个点对，以及一个额外点按验证结果
PnP（Perspective-n-Point）

PnP（Perspective-n-Point）是求解 3D 到 2D 点对运动的方法。它描述了当我们知道n 个 3D 空间点以及它们的投影位置时，如何估计相机所在的位姿。前面已经说了， 2D-2D的对极几何方法需要八个或八个以上的点对（以八点法为例），且存在着初始化、纯旋转和尺度的问题。然而，如果两张图像中，其中一张特征点的 3D 位置已知，那么最少只需三个点对（需要至少一个额外点验证结果）就可以估计相机运动。特征点的 3D 位置可以由三角化，或者由 RGB-D 相机的深度图确定。因此，在双目或 RGB-D 的视觉里程计中，我们可以直接使用 PnP 估计相机运动。而在单目视觉里程计中，必须先进行初始化，然后才能使用 PnP。 3D-2D 方法不需要使用对极约束，又可以在很少的匹配点中获得较好的运动估计，是最重要的一种姿态估计方法

PnP 问题有很多种求解方法，例如用三对点估计位姿的 P3P，直接线性变换（DLT），EPnP（Efcient PnP）等等。此外，还能用非线性优化的方式，构建最小二乘问题并迭代求解，也就是万金油式的 Bundle Adjustment。我们先来看 DLT，然后再讲 Bundle Adjustment

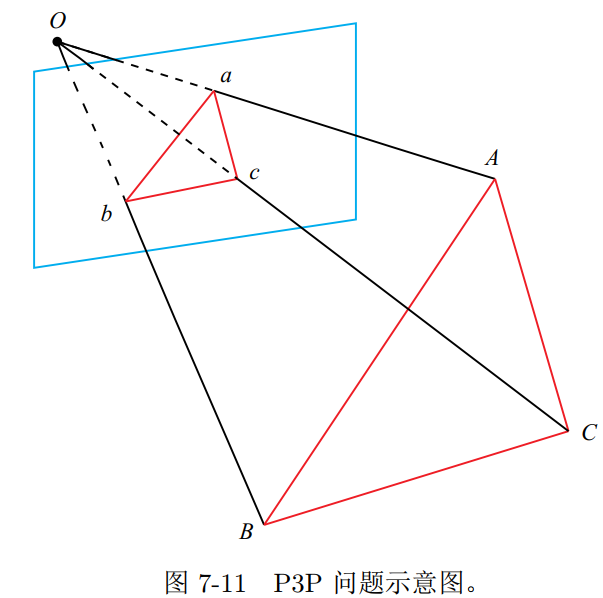
P3P

P3P 需要利用给定的三个点的几何关系。它的输入数据为三对 3D-2D 匹配点。记 3D点为 A; B; C， 2D 点为 a; b; c，其中小写字母代表的点为大写字母在相机成像平面上的投影，如图 7-11 所示。此外， P3P 还需要使用一对验证点，以从可能的解出选出正确的那一个（类似于对极几何情形）。记验证点对为 D − d，相机光心为 O。请注意，我们知道的是A; B; C 在世界坐标系中的坐标，而不是在相机坐标系中的坐标。一旦 3D 点在相机坐标系下的坐标能够算出，我们就得到了 3D-3D 的对应点，把 PnP 问题转换为了 ICP 问题

从 P3P 的原理上可以看出，为了求解 PnP，我们利用了三角形相似性质，求解投影点 a; b; c 在相机坐标系下的 3D 坐标
最后把问题转换成一个 3D 到 3D 的位姿估计问题

Bundle Adjustment （可参考第九讲）

除了使用线性方法之外，我们可以把 PnP 问题构建成一个关于重投影误差的非线性最小二乘问题。前面说的线性方法，往往是先求相机位姿，再求空间点位置，而非线性优化则是把它们都看成优化变量，放在一起优化。这是一种非常通用的求解方式，我们可以用它对 PnP 或 ICP 给出的结果进行优化。这一类把相机和三维点放在一起进行最小化的问题，统称为Bundle Adjustment。

3D-3D: ICP （Iterative Closest Point）

根据配对好的3D点估计相机的运动（已由图像特征给定了匹配的情况下进行位姿估计的问题）

在RGB-D SLAM 中，由于一个像素的深度数据可能测量不到，所以我们可以混合着使用 PnP和 ICP 优化：对于深度已知的特征点，建模它们的 3D-3D 误差；对于深度未知的特征点，则建模 3D-2D 的重投影误差。于是，可以将所有的误差放在同一个问题中考虑，使得
求解更加方便

对极几何->PnP->ICP,在这个过程中我们使用了越来越多的信息（没有深度—>有一个图的深度—>有两个图的深
度），因此，在深度准确的情况下，得到的估计也将越来越准确

小结

本节介绍了基于特征点的视觉里程计中的几个重要的问题。包括：

特征点是如何提取并匹配的；
如何通过 2D-2D 的特征点估计相机运动；
如何从 2D-2D 的匹配估计一个点的空间位置；
3D-2D 的 PnP 问题，它的线性解法和 Bundle Adjustment 解法；
3D-3D 的 ICP 问题，其线性解法和 Bundle Adjustment 解法

第八讲

直接法的引出

在视觉里程计中，除了可以用特征点法，还可以用直接法

我们看到使用特征点确实存在一些问题。有没有什么办法能够克服这些缺点呢？我们有以下几种思路：

保留特征点，但只计算关键点，不计算描述子。同时，使用光流法（Optical Flow）来跟踪特征点的运动。这样可以回避计算和匹配描述子带来的时间，但光流本身的计算需要一定时间
只计算关键点，不计算描述子。同时，使用直接法（Direct Method）来计算特征点在下一时刻图像的位置。这同样可以跳过描述子的计算过程，而且直接法的计算更加简单

第一种方法仍然使用特征点，只是把匹配描述子替换成了光流跟踪，估计相机运动时仍使用对极几何、 PnP 或 ICP 算法。而在直接法中，我们会根据图像的像素灰度信息来计算相机运动。

使用特征点法估计相机运动时，我们把特征点看作固定在三维空间的不动点。根据它们在相机中的投影位置，通过最小化重投影误差（Reprojection error）来优化相机运动。在这个过程中，我们需要精确地知道空间点在两个相机中投影后的像素位置——这也就是我
们为何要对特征进行匹配或跟踪的理由。同时，我们也知道，计算、匹配特征需要付出大量的计算量。相对的，在直接法中，我们并不需要知道点与点之间之间的对应关系，而是通过最小化光度误差（Photometric error）来求得它们。

20210701172116

直接法的推导

我们的目标是求第一个相机到第二个相机的相对位姿变换

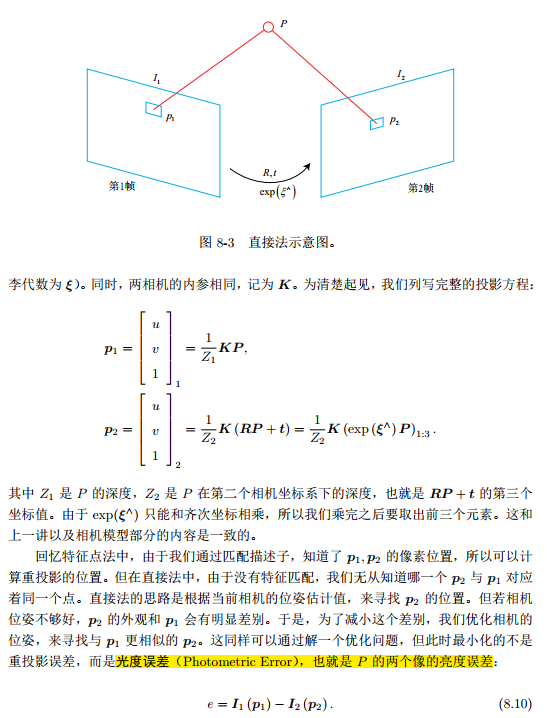
相比于特征点法，直接法完全依靠优化来求解相机位姿。像素梯度引导着优化的方向。如果我们想要得到正确的优化结果，就必须保证大部分像素梯度能够把优化引导到正确的方向。

原理解释（通俗易懂）

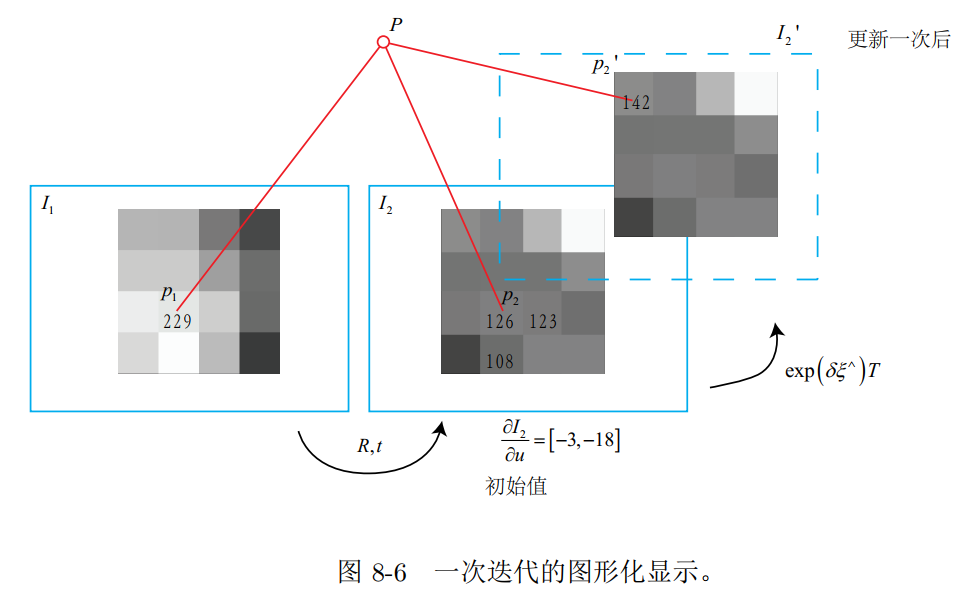
优缺点

20210701185914

前端视觉里程计能给出一个短时间内的轨迹和地图，但由于不可避免的误
差累积，这个地图在长时间内是不准确的。所以，在视觉里程计的基础上，我们还希望构
建一个尺度、规模更大的优化问题，以考虑长时间内的最优轨迹和地图。不过，考虑到精
度与性能的平衡，实际当中存在着许多不同的做法。

第九讲：后端1

Bundle Adjustment （BA）
所谓的 BundleAdjustment，是指从视觉重建中提炼出最优的 3D 模型和相机参数（内参数和外参数）。
从每一个特征点反射出来的几束光线（bundles of light rays），在我们把相机姿态和特征点空间位置做出最优的调整 (adjustment) 之后，最后收束到相机光心的这个过程，简称为 BA。

第十讲

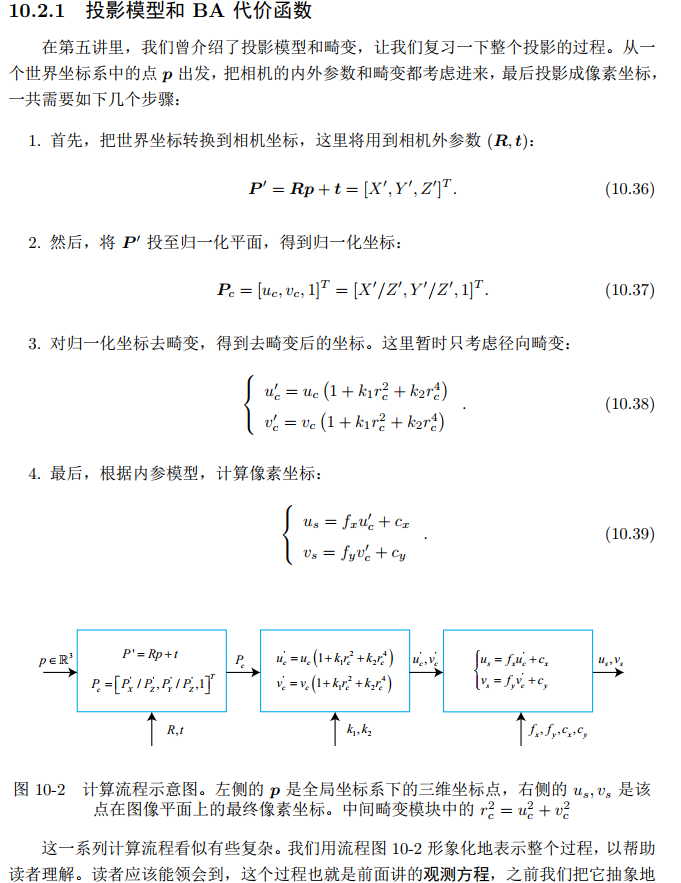
SLAM的主体（前端、后端）主要的目的在于估计相机运动：前端提供特征点的提取和轨迹、地图的初值，而后端负责对所有这些数据进行优化。

第十一讲：回环检测

回环检测模块，能够给
出除了相邻帧之外的，一些时隔更加久远的约束：例如 x1 − x100 之间的位姿变换。为什
么它们之间会有约束呢？这是因为我们察觉到相机经过了同一个地方，采集到了相似的数
据。而回环检测的关键，就是如何有效地检测出相机经过同一个地方这件事。如果我们能
够成功地检测这件事，就可以为后端的 Pose Graph 提供更多的有效数据，使之得到更好
的估计，特别是得到一个全局一致（Global Consistent）的估计
回环检测对于 SLAM 系统意义重大。它关系到我们估计的轨迹和地图在长时间下的正确性。另一方面，由于回环检测提供了当前数据与所有历史数据的关联，在跟踪算法丢失之后，我们还可以利用回环检测进行重定位。因此，回环检测对整个 SLAM 系统精度与
鲁棒性的提升，是非常明显的。甚至在某些时候，我们把仅有前端和局部后端的系统称为
VO，而把带有回环检测和全局后端的称为 SLAM

第十二讲：建图

在适用范围内， RGB-D 相机是一种更好的
选择。在 RGB-D 相机中可以完全通过传感器中硬
件测量得到，无需消耗大量的计算资源来估计它们。并且， RGB-D 的结构光或飞时原理，
保证了深度数据对纹理的无关性。即使面对纯色的物体，只要它能够反射光，我们就能测
量到它的深度。这亦是 RGB-D 传感器的一大优势。
利用 RGB-D 进行稠密建图是相对容易的。不过，根据地图形式不同，也存在着若干
种不同的主流建图方式。最直观最简单的方法，就是根据估算的相机位姿，将 RGB-D 数
据转化为点云（Point Cloud），然后进行拼接，最后得到一个由离散的点组成的点云地图
（Point Cloud Map）。在此基础上，如果我们对外观有进一步的要求，希望估计物体的表面，
可以使用三角网格（Mesh），面片（Surfel）进行建图。另一方面，如果希望知道地图的障
碍物信息并在地图上导航，亦可通过体素（Voxel）建立占据网格地图（Occupancy Map）。

配置ORB-SLAM2

官方源码及环境配置
 ORB-SLAM2 系列博文

pangolin
根据官网安装required and Recommended dependencies。然后编译文件

cd Pangolin
mkdir build
cd build
cmake ..
make
sudo make install

opencv3
- 安装过程遇到的问题解决方案

cd opencv-3.4.15
mkdir build
cd build
cmake ..
make
sudo make install

Eigen3
- 使用sudo apt-get install libeigen3-dev
ORB-SLAM2
- 报错：error: usleep is not declared this scope。其解决方法: 只需在/include/System.h文件中添加头文件#include <unistd.h>即可
在ORB-SLAM2中新建文件夹DataDownload，将数据下载到该文件夹下并解压。用官网的命令行来运行程序

SLAM

SLAM中Jacobian矩阵的表达形式，其他参考
- 2*3的三维点表达
- 2*6的相机位姿表达
相机之间添加约束时的Hessian及边缘化过程
- VSLAM之边缘化 Marginalization 和 FEJ (First Estimated Jocobian)
- SLAM中的marginalization 和 Schur complement

转载规则

《视觉SLAM14讲》由 M 采用知识共享署名 4.0 国际许可协议进行许可。

读“自卑与超越”

书摘人生目标一旦确定，自我训练自然也会随即而来。随着时间的推移，他便会充实自己，提高个人能力，解决生活中的三大问题。我们不妨以爱情及婚姻为例。如果我们关注伴侣，想要伴侣拥有舒适、幸福、丰富的生活，那我们必然会为此全力以赴。如果我们不思贡献

2021-06-20 Growth

Reading List

781-森林中的兔子

781. 森林中的兔子报相同数字的兔子中（如n个兔子报的数字都是m，即[m, m, … m]）如果n+1<=m (如 [6,6]) ,则可以认为这些兔子都是同一种颜色,可以抱成一团,兔子个数为（m+1）*（n//(m+1)

2021-05-25 LeetCode

LeetCode

第二讲

使用库

Quick CMake tutorial及配套代码

CMakeLists.txt示例1

CMakeLists.txt示例2

第三讲

内积和外积

SO（n）和SE（n）

旋转向量 （不紧凑）

欧拉角 （有奇异性）

四元数 （既紧凑，又没有奇异性）

代码调试

第四讲

李群和李代数

李代数求导和扰动模型

SO3，so3，SE3和se3初始化以及相互转换关系

旋转矩阵（R），旋转向量（V）和四元数（Q）在Eigen中转换关系

第五讲

第六讲

第七讲

特征点

2D-2D：对极几何 （7.3节，单目相机）

3D-2D：PnP （7.7节,双目或 RGB-D 相机）

P3P

Bundle Adjustment （可参考第九讲）

3D-3D: ICP （Iterative Closest Point）

小结

第八讲

直接法的引出

直接法的推导

第九讲：后端1

第十讲

第十一讲：回环检测

第十二讲：建图

配置ORB-SLAM2

SLAM

A cup of coffee？

旋转向量（不紧凑）

欧拉角（有奇异性）

四元数（既紧凑，又没有奇异性）

2D-2D：对极几何（7.3节，单目相机）