方法1:dp数组未优化的暴力解法(会超时)
分成两个子楼重新按照1层计数
- dp数组的含义:dp[i][j]表示i个蛋,要确定j层楼,最小的扔鸡蛋次数
class Solution(object):
def superEggDrop(self, k, n):
"""
:type k: int
:type n: int
:rtype: int
"""
dp = [[float('inf') for _ in range(n + 1)] for _ in range(k + 1)]
for i in range(1,n + 1):
dp[0][i] = 0
dp[1][i] = i
for i in range(1,k + 1):
dp[i][0] = 0
dp[i][1]=1
for i in range(2, k + 1):
for j in range(2, n + 1):
for t in range(1,j+1):
dp[i][j] = min(dp[i][j], max(dp[i - 1][t-1], dp[i][j-t]) + 1)
return dp[-1][-1]
# if __name__ == '__main__':
# k1=2
# n1=6
# so=Solution()
# print(so.superEggDrop(k1,n1))
方法2: 用一个k状态优化方法1的第三层for循环 (todo)
choosing k_1…k_N for each dp[i][1…N]
To go one step further, till now, we are still finding the optimal floor k from 1 to j for each dp[i][j]. But is this really the smallest range we can narrow? In fact, we can see that the optimal floor k for each dp[i][j] increases as j increases. This means that once we get the optimal k for dp[i][j], we can save current k value and start the next round of for-loop directly, instead of initiating k from 0 again. In this way, in the third for-loop, k will go from 1 to N only once as j in the second for-loop goes from 1 to N. The total time complexity will be O(kn). The code is shown below:
class Solution(object):
def superEggDrop(self, K, N):
"""
:type K: int
:type N: int
:rtype: int
"""
dp=[[float('inf')]*(N+1) for _ in range(K+1)]
for i in range(1, K+1):
dp[i][0] = 0
dp[i][1] = 1
for j in range(1, N+1):
dp[1][j] = j
for i in range(2, K+1):
k = 1
for j in range(2, N+1):
while k < j+1 and dp[i][j-k] > dp[i-1][k-1]:
k += 1
dp[i][j] = 1 + dp[i-1][k-1]
return dp[K][N]
方法3:换个角度定义dp数组的含义
I think we should keep in mind what the dp[m][k] means, it means the highest levels we can confirm. Then, we take 1 move to a floor and the egg will break or not. If the egg breaks, it means we should find the answer under this level, and it also means this level can not be higher than dp[m-1][k-1] + 1, otherwise we will unable to get the answer. If the egg doesn’t break, we will use the k eggs and m-1 moves to go higher. So the highest level we can touch is dp[m-1][k-1] + 1 + dp[m-1][k]. We can find the answer use k eggs and m moves in any level which not higher than it.
始终把楼当成整体
- dp数组的含义:dp[i][j] 表示用j个鸡蛋扔i次可以测出的最大层数(题目求k个鸡蛋,扔多少次,可以测出(超过或等于)n层)
Q:为什么dp[i][j]数组不定义为用i个鸡蛋扔j次可以测出的最大楼层?(其实也可以,但需要竖着遍历table,有点别扭)
A: 假设1个蛋扔5次可以测出n层,5个蛋扔2次也可以测出n层。由于问题是求扔的最少次数,所以我们取的是5个蛋扔2次。因此,每一行表示扔的次数,每一列表示鸡蛋数。在横向遍历dp table时,取到2次5蛋时,return 即可。- 如果不想纠结i和j哪个是蛋数,哪个是扔的次数,把for循环改为
while(dp[i][j]<n)循环即可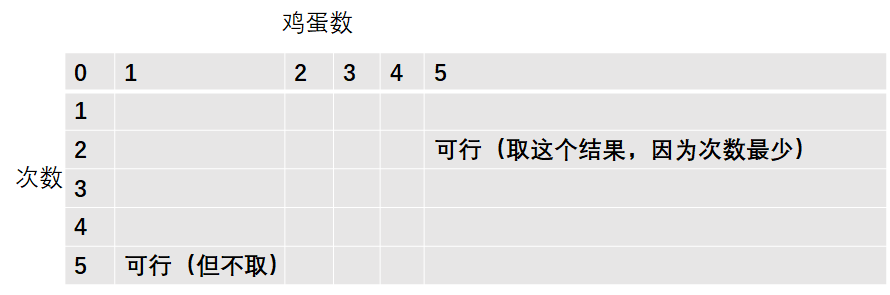
- 如果不想纠结i和j哪个是蛋数,哪个是扔的次数,把for循环改为
- 鸡蛋没碎,鸡蛋数量不变,可用次数减一,dp[i - 1][j](能测到的最大上层)
- 鸡蛋碎了,鸡蛋数量减一,可用次数减一,dp[i - 1][j - 1](能测到的最大下层)
- 1(当前层)
- 最大层数 = 上层 + 下层 + 当前层
- 当能测到大于等于n层时,返回i(也就是扔的次数)
class Solution(object):
def superEggDrop(self, k, n):
"""
:type k: int
:type n: int
:rtype: int
"""
dp = [[0] * (k + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
for j in range(1, k + 1):
dp[i][j] = dp[i - 1][j - 1] + 1 + dp[i - 1][j]
if dp[i][k] >= n:
return i
//#include<iostream>
//#include<string>
//#include <vector>
//
//using namespace std;
class Solution {
public:
int superEggDrop(int k, int n) {
vector<vector<int>> dp(n + 1, vector<int>(k + 1, 0));
for (int i = 1; i < n + 1; ++i) {
for (int j = 1; j < k + 1; ++j) {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] + 1;
if (dp[i][k] >= n) {
return i;
}
}
}
// 不加这一行,本地编译器可以通过
// 但在leetcode上编译时(编译器更严格),// 这一行一定要加,随便return个数字就行, return 100之类的
return n; // 加这一行只是为了编译通过。函数实际上返回的是i。
}
};
//int main() {
// int k = 2, n = 6;
// Solution s;
// cout << s.superEggDrop(k, n) << endl;
//
//}




