解析递归和回溯的关系
递归
递归就是把大问题对应的小问题解决后(注意:大小问题结构一致),再根据小问题的结果完善大问题。遇到递归问题,要想明白:
- 递归函数的含义:这个函数要实现什么功能?返回什么结果?(一定不要跳进递归,相信这个函数能返回你需要的东西)
- 这个函数的变量:什么变量会导致结果变化?比如如果是二叉树的递归,就要想清楚这个二叉树的的节点的变量是什么
- 得到递归结果后,要干什么:如何把递归结果变成题目要求的结果?
- 递归结束的条件:递归出口
以盖房子这道题为例:
- 含义:给定一个节点,返回n次后的房子排列
- 变量:在这个二叉树中,各个子树的节点颜色是变化的,子树的盖房子次数是变化的,所以递归函数的签名写为
def helper(n,color) - 干什么:以父节点为例,它的左子节点颜色为G,右节点颜色为R(并且相信左右子树能返回我要的结果)。因此根据题意进行中序遍历:左子树的结果+自己+右子树的结果
- 结束条件:盖一次自己(已到达叶子节点)
以78. 子集的递归写法为例:
- 含义:返回的子集结果
- 变量:nums。父nums和子nums相差一个元素
- 干什么:在得到子结果后,追加新的结果
- 结束条件:nums为空
回溯
回溯算法的框架
result = []
def backtrack(路径, 选择列表):
# 递归的出口
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
# 做选择, 类似前序遍历
将该选择从选择列表移除
路径.add(选择)
# 相信它能返回我这次选择后需要的结果
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表回溯算法其实也是一种递归。在父递归函数中有一个for循环,for循环里面调用子递归函数。以全排列的这段代码为例:
def backtrack(nums,visited):# 选择列表和路径
if len(visited)==len(nums):
res.append(visited[:])
return
for num in nums:
if num in visited:
continue
else:
visited.append(num)
backtrack(nums,visited)
visited.pop()- 含义:返回某个节点对应的全排列
- 变量:在每个节点处,当前的选择列表和已经走过的路径
- 得到结果后,返回即可
- 递归结束的条件:已经到达了叶子节点
在全排列中,以最左侧的节点1为例,在根节点选择了1后,for循环里的backtrack(nums,visited)可以返回以1为基础的全排列。然后通过visited.pop(),现在重新回到根节点,进行第二次for循环,选2。以此类推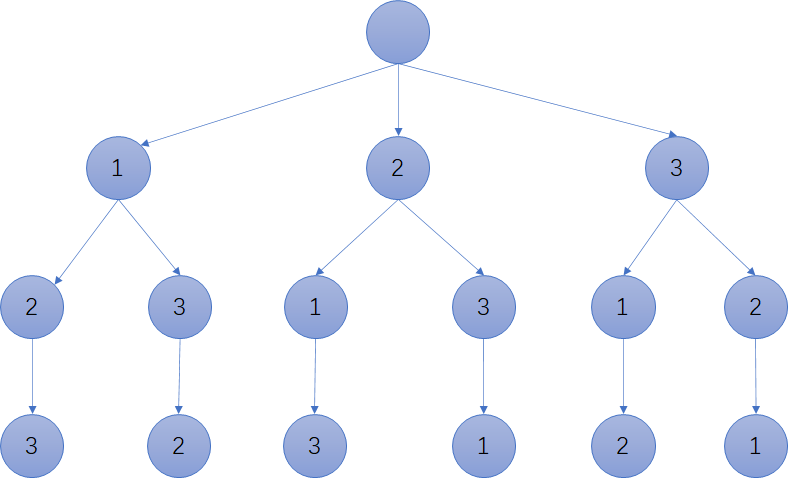
更新选择列表的方式
在回溯算法的for循环中,常常用两种方式更新选择列表
- 第一种:若选择已经在走过的路径中了,则跳过该选择
for num in nums:
if num in visited:
continue
else:
...for (int num :nums) {
// 检查当前num是否在路径中,count返回0(不在)或1(在)
if (count(visited.begin(), visited.end(), num))
continue;
- 第二种:通过一个start标志位来剪枝不可行的子树(小于当前选择的选择全部剪掉)
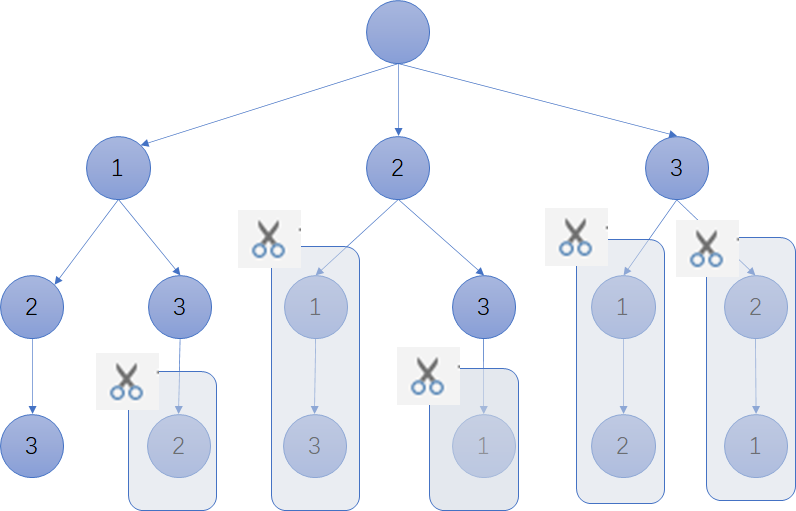
for i in range(len(nums)):
# 做选择
visited.append(nums[i])
res.append(visited[:])
# 回溯,用nums[i+1:]更新选择列表
backtrack(nums[i+1:],visited)for (int i = start; i < nums.size(); ++i) {
visited.push_back(nums[i]);
res.push_back(visited);
//后面的dfs过程,只能选择nums[i+1:]范围的元素
dfs(nums,visited,i+1);
visited.pop_back();在这些题目中:
- 46题全排列就是用的第一种,已经走过的路径就不选了
- 78题子集和77题组合就是用的第二种,小于当前选择的选择就不选了。
- 78题和77题的不同之处在于:
- 78题结果中记录的是每个节点对应的路径,在没有选择时(
if not nums)跳出 - 77题结果中记录的是路径长度等于k时的路径,因此在
if (visited.size()==k)时,记录当前路径并跳出
- 78题结果中记录的是每个节点对应的路径,在没有选择时(




